题记
本文写于三年前当我正在初步学习量子信息和量子计算理论时期,国际上又发生了一些事关网络信息安全的事件。今日看来,当时的一些想法或许有些欠成熟,很多涉及量子计算优越性本质的特性(比如量子系统张量乘积的维数递加现象,可逆性,低能耗性)也未得到深入探讨,不过整体来看也许会对相关领域的初学者有一定的借鉴价值,而该领域的一些关键问题也远未得到圆满解决的共识。于是决定现把拙文放到这里,仅供参考,亦欢迎斧正。
导言
2013年5月Google和NASA等宣布将联合成立量子人工智能实验室,他们将使用的量子计算机将是由D-wave公司制造的D-wave Two量子计算机。D-wave Two是继2011年5月卖给美国著名军火制造商洛克希德·马丁公司的世界上第一台商业量子计算机D-wave One的升级版。相比拥有128量子比特位的D-wave One系统, D-wave Two的计算核心超导电子芯片拥有512个量子位,计算芯片同样只有拇指大小,需要的工作温度也只高于绝对零度20微开尔文(\(2\times 10^{-5}K\)),其整个机柜大小相当于一个大型冷藏柜。而在对D-wave Two的性能测试中。D-wave Two平均仅用了不到半秒钟的时间就可以得到销售路线优化问题的最优解。而当时作为参照组的一个高性能经典(classical)计算机集群最快也要大概30分钟才能算出最优解。按照这个结果推算,D-wave Two量子计算机大概能够排到2012年11月发布的世界最快超级计算机排名表上的第十名。相比于一般超级计算机的巨大占地面积和功耗,D-wave Two实在是一个计算能力超强的小蚂蚁。按照预测量子计算机发展的“肉丝”定理(音译Rose’s Law),量子计算机的运算性能将在2014年前后超越所有的经典电子计算机,这也是D-wave正在开发制造的具有更高量子比特位的下一代量子计算机。同时,美国自然基金、军方和一些私募基金已经在研制可以破解当前绝大部分信息加密算法的量子计算机方面投入了大量的研究资助。一旦具有大数分解能力的量子计算机研制成功,我们现有的金融、通信等方面的加密机制将无法实现保密的目的。当然,好的方面是,目前难以求解的一些科学问题也很可能会在量子计算机的帮助下得以快速破解。
为什么量子计算机具有这么强大的计算能力?为什么量子计算机会得到Google和其他前沿研究机构的青睐?笔者在这里将结合量子科技最近几年快速发展的形势,简单谈一谈量子计算和量子信息处理的一些基本知识和可能应用。
强劲量子计算源于物理世界的智慧
从信息单元上说,相比于经典计算机采用逻辑状态或者比特位(bit)作为信息单元的信息结构,量子计算机或者量子信息处理系统使用量子比特(qubit)作为信息单元。如果用0和1表示传统经典计算机的一个比特可以表征的信息,一个量子比特位可以同时表征0和1两个状态的叠加。通常我们使用狄拉克括号“\(\lvert *\rangle\)”来表示一个量子态,以区别于传统的计算机逻辑状态。任何一个量子态\(\ket{\Psi}\)都可以写成量子0态\(\ket{0}\)和量子1态\(\ket{1}\)的叠加。也就是说,如果写成数学式的形式,任意量子态可以表示成:\(\ket{\Psi}=a\ket{0}+b\ket{1}\)。其中\(a=\bra{0}\Psi\rangle\)和\(b=\bra{1}\Psi\rangle\)称之为这个量子态在量子态\(\ket{0}\)或\(\ket{1}\)上的概率幅。简单的说,这个量子状态实际上就是按照一定的概率分布可以同时出现在基本状态\(\ket{0}\)或者\(\ket{1}\)上的一种特殊叠加状态。其出现在\(\ket{0}\)上的概率为对应概率幅的模方(绝对值的平方),即得到\(\ket{0}\)的概率\[P(0)=P(0\lvert\Psi)=|a|^2=\lvert\langle 0\vert \Psi\rangle\rvert^2.\] 相应的,出现\(\ket{1}\)的概率为\[P(1)=P(1\vert \Psi)=|b|^2=|\langle 1\vert \Psi\rangle|^2.\] 其中我们定义\(P(c\vert \Psi)\)表示当输入状态是\(\ket{\Psi}\)的条件下测得状态\(\ket{c}\)的概率,而\(c\)可以是\(0\)或者\(1\)。按照一个只包含\(\ket{0}\)和\(\ket{1}\)两个基本状态的量子叠加态出现在这两个状态上的总概率必然为\(1\)的定义,我们可以得出概率幅的一个基本守恒关系,即\(P(0\vert\Psi)+P(1\vert\Psi) =|a|^2+|b|^2=1\)。
下面举个简单的例子来说明物理上如何实现这种具有叠加态的量子比特,及其这种叠加态不同于传统经典逻辑状态的一些性质。如图1所示,假设我们有一个光子(光的最小能量单元)入射到一个分束器上,该光子按照一定的比例分成了两种传播模式:我们定义垂直向上传播的光子态为\(\ket{0}\)态,水平传播的光子态为\(\ket{1}\)态。假设这个分束器允许光子按照原方向传播的概率为T,允许光子沿\(90^\circ\)角反射传播的概率为R,那么一个入射光子态为\(\ket{1}\)(水平传播)的光子经过该分束器后的量子态为\(\ket{\Psi}=r\ket{0}+t\ket{1}\),这里\(|t|^2=T\)及\(|r|^2=R\)满足\(T+R=1\)的概率守恒条件。也就是说,任意一个量子态都可以通过这种利用改变分束器反射率或透射率的方法经分光得到。一般的,入射光可以是\(\ket{1}\)态(水平入射),也可以是\(\ket{0}\)态(竖直入射),这样通过分束器同样可以产生任意状态的量子态。当然,量子态只是一个抽象的概念,可以通过其他很多种方法产生,这里不再一一阐述。因为用上述光学方法产生量子态的方案比较直观而简单,我们继续基于这种方案探讨下量子态叠加的一些有趣性质。
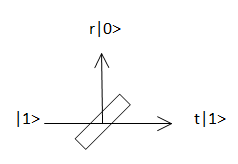
图 1:用分束器产生量子态示意图。矩形模块表示分束器,直线表示光路。

图 2:光子干涉装置示意图。空白矩形模块表示分束器,带斜纹的矩形模块为反射镜。光从左下端入射。
如图2所示,在光路中我们对称的加入两个分束器和两个全反射镜片。光子从左下端口入射,经过第一个分束器之后产生了一个量子初态,然后分别经过两个对称的全反射镜后两个光路的传播方向交换,产生对第二个分束器的入射初态\(\ket{\phi}\);这个量子态经过第二个分束器分束,最终产生了最终的出射量子态\(\ket{\Psi}=\alpha\ket{\phi_\alpha}+\beta\ket{\phi_\beta}\)。其中\(\ket{\phi_\alpha}\)和\(\ket{\phi_\beta}\)是两个相反的状态,分别可以是\(\ket{0}\)或者\(\ket{1}\)态或者两个基本态的叠加态。这个装置的本质功能是实现量子态之间的干涉叠加。假设我们想知道出射量子态是\(\ket{a}\)的概率\(P(a\vert\Psi)\)。这里\(a\)可以是\(0\)也可以是\(1\)。那么这个概率可以用数学式写成 \[\begin{align} &P(a\vert\Psi)=|\langle a\vert\Psi\rangle|^2=|\alpha\langle a\vert\phi_\alpha \rangle +\beta\langle a\vert \phi_\beta \rangle |^2\\ =&|\alpha|^2 \vert\langle a\vert \phi_\alpha \rangle |^2+|\beta|^2 \langle a\vert \phi_\beta\rangle |^2+\alpha\beta^* \langle a\vert \phi_\alpha\rangle\langle\phi_\beta \vert a\rangle+\alpha^* \beta\langle a\vert\phi_\beta\rangle\langle\phi_\alpha\vert a\rangle\\ =&\color{blue}{P(a\vert\phi_\alpha)P(\phi_\alpha\ket{\Psi}+P(a\vert\phi_\beta)P(\phi_\beta\vert\Psi)} +\color{red}{\alpha\beta^* \bra{a}\phi_\alpha\rangle\langle \phi_\beta\ket{a}+\alpha^* \beta\langle a\ket{\phi_\beta}\langle \phi_\alpha \ket{a}} \end{align}\] 上面我们已经用到了复数模方的一些简单运算性质,星号上标表示取复共轭或者厄米共轭的运算。上式的第一项的数学意义为\(\ket{\Psi}\)含有\(\ket{\phi_\alpha}\)的概率与\(\ket{\phi_\alpha}\)含有\(\ket{a}\)态概率的乘积。第二项表示\(\ket{\Psi}\)含有\(\ket{\phi_\beta}\)的概率与\(\ket{\phi_\beta}\)含有\(\ket{a}\)态概率的乘积。后面两项成为光子干涉项。由条件概率乘积的性质可以知道,上式前两项(我们称之为经典项)已经从逻辑上完整的表示了\(\ket{\Psi}\)含有\(\ket{a}\)态的概率\(P(a\vert\Psi)\)!然而从以上严格的推导来看,\(P(a\vert\Psi)\)除了两个逻辑项外,还包含两个干涉项,而这两个干涉项在\(\ket{\phi_\alpha}\)和\(\ket{\phi_\beta}\)均是\(\ket{0}\)与\(\ket{1}\)叠加态的情况下是不为0的!这种不符合经典逻辑概率关系的干涉性质正是量子态不同于经典逻辑态的一个基本性质,也是导致量子计算及量子信息处理可以具有超越传统经典计算机的一个根本所在。
不仅限于状态叠加带来的于众不同的物理和数学性质,量子及广义概念上的物理世界里还有更多经典计算机不具有的性质被运用到了量子计算机的发展过程中。比如量子纠缠态这种现象,即两个物理体系(比如一个电子和一个光子)具有一定的关联关系的状态。当一个光子和一个电子形成纠缠态后,当一个光子被测量之后,电子可以唯一确定的立即塌缩到某个态上。利用量子纠缠这种性质,量子计算机可以将原来经典计算机要使用大量计算步骤甚至近乎无穷长的时间才能计算出来的问题只使用有限的几步快速解决掉。这通常被称为量子计算的指数加速性质。对应已知的具有指数加速性能的量子算法包括Shor的因式分解算法,Grover的检索算法等等。利用量子纠缠性质,人们也可以去实现更加安全的量子加密和量子保密通信。我国将在2016年发射的首颗量子通信实验卫星以及已经在芜湖和济南建成的量子通信实验网络就是利用这些量子物理性质实现的保密通信系统。相比于传统的依赖于数学加密算法的通信系统,量子保密通信系统彻底的杜绝了利用数学算法对通信内容进行密码破解的可能,是一种从物理层上实现信息加密的新型通信体系。
众所周知,物理世界的自然定律认为大自然具有天然的寻找“最优解”的能力。比如,光总是沿着“最短路径”前进,任意物理系统总是向着能量最低态演化等等。量子计算机发展之初正是借助了这种物理世界赋予的内在优化能力向着模拟自然世界本身及解决各种优化问题为出发点的。D-wave生产制造的量子计算机也正是专门为解决优化问题而设计的。利用他们的量子计算机,只要你将问题等价为一个物理演化问题,输入对应的物理描述,量子系统就会自动向着最优化的结果自动演化,然后通过反演得到对应数学问题的解。
回顾量子计算机的发展历程,可以说自从主要的量子信息和量子计算的概念在上世纪七八十年代被提出伊始,人们就开始考虑如何利用自然界的物理定律和物质的物理性质来重新理解信息处理和计算的本质,并试图重构其数学基础。相比而言,传统经典计算机的提出却恰恰是先提出了图灵机这类纯数学的概念,然后才去寻找可以利用的物理载体进行信息处理和计算的应用。经过几十年来人们对计算和信息处理本质理解的加深,以及对物理世界普遍存在及成立的量子物理理论和微观物理体系操纵能力,特别是对纳米、超导和原子系统操纵能力的提高,量子计算机和量子信息处理系统作为这一过程的智慧和工程结晶自然会产生超越经典电子计算机的综合性能。而目前D-wave制作的量子计算机也从实践上证明了这种优越性。
量子人工智能和大数据处理
在过去的几十年里,人们对计算和信息处理本质的理解不仅仅局限在量子物理领域,而且扩展到对人脑和认知科学等领域。通过对人脑学习过程和神经系统运行机制的研究,科学界逐渐总结发展出了人工智能和机器学习等领域。众所周知,人的大脑具有数千亿以上的神经元,其间具有着极其复杂的神经网络,他们又不断地收集着来自广泛分布于人身体各个组织器官上数不清的“传感器”发送来的实时信号,并实时处理信息然后将控制信号发送到数不清的神经末梢及控制单元上实现着人体的各种机能和运动。这一系统对处理当今世界上的大量数据信息具有直接的指导意义。比如说,广泛分布在全国各个街道上的摄像头和传感器不断地收集着来自各条道路节点上的实时交通运行视频信息及传感信号,其信息量是巨大的、连续的。如果要使用人工不间断的监视这些信息信号,一方面很容易人为地遗漏掉一些关键情况,另一方面这是难以实时完成的。对待这样的信息处理案例,只能大量借助智能化、自动化的信息处理方法才能保证实时完成。对于大数据处理,常用的机器学习算法包括两类,一是有监督的机器学习算法,另一个是无监督的机器学习算法。实际上,我们日常使用的很多网上商城提供的商品推荐系统等正是一种主要依赖于无监督和一定的有监督的机器学习算法的应用:等你评价已经购买的商品的好坏之后,计算机系统会对你的偏好进行分析,并将类似于你喜欢的商品自动推荐给你。而相当一部分邮件服务商提供的垃圾邮件自动分类系统等是使用了有监督的机器学习算法的结果:等你对某些邮件归入垃圾邮件范畴之后,你已经告诉了计算机系统垃圾邮件有哪些特征,计算机会根据你的分类自动将未来符合垃圾邮件特征的邮件放到垃圾邮件文件夹。还有手写识别系统,这基本上是应用了有监督机器学习算法的应用等等。
然而面对数据量极大的情况,即使使用世界上最快的电子计算机,有时也很难及时处理这些信息。比如去年确认“上帝粒子”希格斯子存在的大型强子对撞机(LHC)每秒有60亿次的粒子碰撞事件发生(其中只有百万分之一的碰撞事件是有效的),探测器只选择其中的万分之一的碰撞进行数据采集,这样每秒也会产生100Gb的信息需要记录存储,然后让具有15000个CPU的电子计算机再随机选取其中百分之一的数据实例转移给拥有73000个CPU的超级计算机加以分类存储,并以平均10Gb/s的全球数据链路传输速度通过多个线路向全世界科学计算节点分发数据,让150万人使用先进的经典算法进行科学计算,即使如此,这些数据仍然不能实现实时的完整分析。 在近几年,结合机器学习和人工智能原理的量子计算方案已经被提出,比如Seth Lloyd等提出的量子机器学习算法。这些量子算法已经被从理论上证明,他们相对经典计算机的机器学习算法具有指数加速优势。也就是说,很多经典机器学习算法需要1万年才能处理的大数据情况,可以通过相应的量子算法用1秒钟快速解决。
量子技术对隐私的保护及对国家安全的影响
按照Google和NASA成立量子人工智能实验室的官方网站的说法,他们要利用量子计算机进行更好的人工智能算法加强对网络信息的处理能力,同时开展比如太空探索任务规划等算法的开发等等。联系到实际上前3态量子计算机除一台放置于南加州大学用于科研之外,有两台卖给了具有军工背景的美国单位或者网络寡头公司,以及美国最近被揭露的“棱镜”(PRISM)监控计划,笔者认为这些量子计算机很可能将被用于美国的军工及网络监控等方面的应用。而据一些公开的报道,当Seth Lloyd向Google提供他提出的量子搜索算法时,Google的决策者并没有认可使用他的算法。尽管Seth Lloyd的算法出众,但是其算法从物理本质上隐藏了用户的个人信息,只对要检索的信息进行检索,然后Google的掌管人正面指出他们需要的是能够在检索时记录用户所有个人信息的检索算法。所以我们推测Google也正是在开发更容易探查管理用户信息的新型量子算法。
然而从理论上讲,量子计算技术又是实现信息安全突破的关键技术。利用量子态叠加的根本性质,量子信息处理完全可以在隐藏了个人信息的基础上实现快速的信息检索等功能,而且目前学术界已经有了一定的理论基础。按照笔者的理解,简单的说,一种可能的量子检索算法可以抽象地理解信息的内容和问题的本质,摆脱语言和形式的限制,而不是仅仅局限于对关键字的检索。当我们去寻找互联网上某个问题的答案时,量子计算机利用这类算法直接将互联网上公开提供的海量信息快速总结出来,分析得到最准确的答案,其结果可能是综合了很多网站信息的合成,而不仅仅来自于某一个网站;而现在的Google等搜索引擎,检索信息时需要按照关键字出现的情况列出相关的网站,并且根据个人和所在地域检索历史及网站之间的引用情况对检索结果排序,然后让人逐条点击进入人工寻找答案。也许大家没有意识到,由于信息检索在网络信息时代的普及,你所检索的每一条信息都暴露了你每天的所思所为,信息检索引擎也正逐步成为国际社会关注个人信息保护的一个焦点。而利用量子计算技术,不仅检索信息针对需要检索的问题进行了快速广泛的查找和准确定位总结,而且不需要依赖并存储个人检索历史并对最佳答案进行“猜测”筛选,从本源上避免了个人检索历史和其他隐私信息被其他机构恶意利用的风险。量子计算的态叠加性质和指数倍提速是实现这种方案的关键所在,这也是经典计算机难以比拟的优势。
21世纪的计算和信息处理技术就像20世纪的原子能技术,既可以用于建造核电站,也可以用于制造核武器。作为计算及信息技术的制高点,量子计算机及量子通信系统在国家发展及国家安全方面具有极其重要的地位。但该技术向着哪个方向发展亦受着资助者和研究者的极大影响。特别对于保护个人隐私方面防止信息霸权方面,利用量子效应对通信系统的物理层加密,以及能否利用量子技术摆脱个别国家集团对民众隐私信息的窥探等正逐步成为世界民众关注的焦点。我国在量子通信方面已经起步,而且部分领域保持先进水平,但是在量子计算方面先机已经被美国加拿大等国抢占,而且很这方面可能向着对我们不利的方向发展。截至2013年6月,D-wave已经注册了超过100个有关量子计算的专利,相关的应用也会随着Google等的持续开发向着对其商业和政治利益有利的方向深入发展。然而这些利益的争夺是具有战略垄断和技术保密性质的。另一方面,即使我们普及了量子保密通信系统,但只要我们还要去访问他国的服务器,我们的信息就会留在他国的服务器上,目前已知的计算机后门程序和监听软件就会发挥作用,人民的信息安全仍然无法保证。从一定程度上说,信息安全与国家在世界上的整体实力和互联网运营商的可控资源量直接相关。这些都需要得到大家的深入了解,舆论和资源支持,以及未来学子和技术人才不断地深入研究和技术发展。
量子计算技术未来发展展望
虽然量子计算机的商业化发展已经展开,但是目前已经开发的产品只适用于针对个别优化问题的解决,尚不具备通用计算能力。本质上,D-Wave所谓的量子计算机,不过是一种量子退化算法模拟器,只能用于个别优化问题的求解。通用量子计算仍然是近几年的发展趋势,尚存大量的理论和实践问题需要解决。而最近世界上首个将原子集成到光子晶体波导上及长相干量子点器件等的实验突破又为借助现有光通信系统和半导体平面技术实现新型量子计算机和量子通信系统的物理实现展现了希望的曙光。总之,作为一个年轻的研究领域,量子计算正迎接着一次次的突破和创新。
致谢
本文作者特别感谢马磊等朋友对本文撰稿和ICIQ开源社区搭建提供的无私帮助。
参考文献:
How Quantum Computers and Machine Learning Will Revolutionize Big Data.
Seth Lloyd, Programming the Universe: A Quantum Computer Scientist Takes on the Cosmos, Vintage (March 13, 2007)
Scott Aaronson,Quantum Computing since Democritus, Cambridge University Press (March 14, 2013) (早期的在线版见这里).
Michael A. Nielsen and Isaac L. Chuang,Quantum Computation and Quantum Information,Cambridge University Press; 10 Anv edition (January 31, 2011)
Seth Lloyd,Masoud Mohseni,and Patrick Rebentrost. Quantum algorithms for supervised and unsupervised machine learning,2013(arXiv:1307.0411)
Patrick Rebentrost, Masoud Mohseni, Seth Lloyd,Quantum support vector machine for big feature and big data classification,2013(arXiv:1307.0471)
Seth Lloyd, Masoud Mohseni, Patrick Rebentrost,Quantum principal component analysis,2013(arXiv:1307.0401)
Jacob Aron,Quantum links let computers understand language,New Scientist,Volume 208, Issue 2790, 2010, Pages 10–11。
A. Goban, C.-L. Hung, S.-P. Yu, J. D. Hood, J. A. Muniz, J. H. Lee, M. J. Martin, A. C. McClung, K. S. Choi, D. E. Chang, O. Painter, H. J. Kimble,Atom-Light Interactions in Photonic Crystals,2013(arXiv:1312.3446)
一些值得推荐的在线教程笔记和教学视频和习题: John Priskill的在线教程、 Carlton Caves关于量子信息的在线教程视频。